波動伝ぱと材料の粘弾性特性

材料や構造物に振動や衝撃などの動的な力が加わった場合，静的な力がゆっくり加わったとき場合とは異なった挙動を示します．特に，高分子材料や複合材料では，この傾向がより顕著になってきます．材料の動力学的特性を調べる方法はいろいろありますが，ここでは波動伝ぱによる方法を紹介します．

衝撃力や超音波によって，材料中に応力波を発生させると，材料の動力学的性質の影響によって，波形は伝ぱするにしたがい変化していきます．この波形変化を観察し，周波数周波数分析することによって，材料の動力学的性質を調べる方法です．

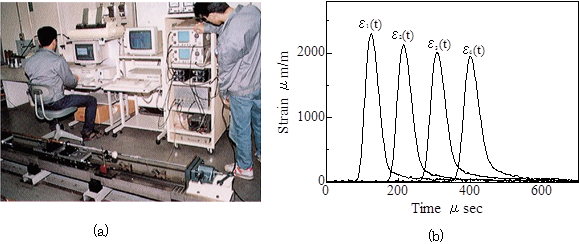
図1　衝撃実験

図1(a)では，高分子材料の丸棒に弾丸を衝突させて応力波を発生させ，波形変化を観察しています図1(ｂ)の．実験結果を見ると，応力波が伝ぱにしたがい減衰いていく様子がわかります．金属棒のような弾性体では，このような波形変化はほとんど観察できません．

このような衝撃試験からは，周波数が15ｋHz程度までの動力学的特性を調べることができますが，固体どうしの衝突ではそれ以上の高周波成分を含む波を発生させるのは困難です．より高周波領域の特性を調べるために，図2(a)のように，超音波振動子によって試料棒に超音波を発生させて，その波形変化を観察します．図2(ｂ)は40ｋHzの超音波振動子を用いた時の実験結果を示しています．伝ぱにしたがい超音波が減衰・分散していていく様子わかります．このような実験を超音波振動子取り替えて次々と行い，25-200ｋHzの範囲で行います．

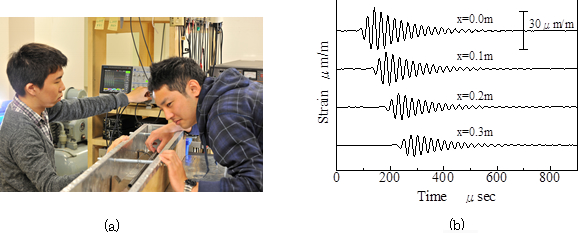
図2 超音波実験

図1（b）や図2(b)のような実験結果をフーリエ周波数解析し，周波数成分ごとの減衰係数と波の伝ぱ速度（位相速度）を算出すると図3，図4に示すプロットのようになります．減衰係数や位相速度が，図3，図4のような周波数特性を持つ結果となったということは，試料として用いた高分子材料の動力学的特性は"弾性だけ"で表すことができないということになります．

このような波動の減衰や分散といったような現象は，"粘弾性"という性質でうまく説明することができます．図5は，その一種で5要素モデルといわれるものです．粘弾性材料中の波動を理論的に解析し，図3，図4の実験値の傾向を再現するように5要素モデルの各パラメータを決めると．図5に付記した値となり，これで材料の動力学的特性が決まったことになります．（なお，波動の分散は，粘弾性の影響のほかに，幾何学的要因によっても左右されるので，そう簡単ではありません．）

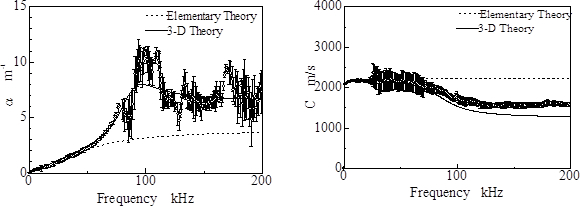
図3 減衰係数　　　　　　　　　　　　　　　　図4 位相速度

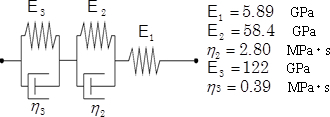
図4 　5要素粘弾性モデル

布地の成形シミュレーション

RTM(Resin Transfer Molding)では，強化繊維布の織り方や初期方位，工具の形状などにより変形が大きく異なります．成形後の繊維方向は複合材料の機械的特性に，織目の形状は樹脂注入時の浸透性に影響を与えます．これらのことを予測するため，布地の成形シミュレーションを安価に行う手法を開発しています．

シミュレーション手順

(1) 織り構造を考慮した布地のモデル化
交点の特性を変えることにより平織り/朱子織に対応可能（図1参照）
　↓
(2) 地の引張り試験とシミュレーションの比較により布地の物性値を決定（図2参照）
　↓
(3) 布地の成形シミュレーション（図3参照）
　↓
(4) 評価・設計変更
　　例えば，交点での滑り量を評価可能(図4参照)

図1 布地の交点のモデル　　　　　　　　　　　図2 布地の引張りシミュレーション

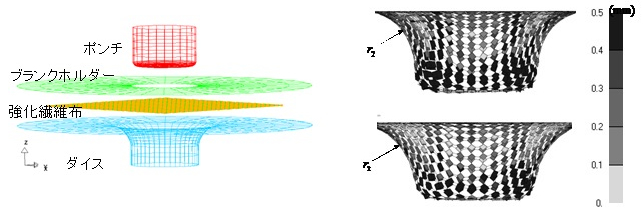
図3 円筒ポンチによる深絞りシミュレーション　　　　　　　　　図4 交点における滑りの分布（側面図）

マイクロポーラ材料の位相形態最適化

マイクロポーラ材料とは

微細構造を持つ材料の力学的挙動を連続体近似する手法の一つにマイクロポーラ弾性理論があります．古典弾性理論では物体中の微小要素に応力が作用すると要素の４辺の平行性が保持されて変形します（図１参照）．マイクロポーラ弾性理論では，図２のような偶応力を導入して微小要素に曲げの変形モードを付加します．このように古典弾性論を拡張すると，「引張りと曲げとが異なる特性を持つ材料」を定義できます．例えば，骨やコンクリートがマイクロポーラ材料として知られています．

図1　応力（単位面積当たりの内力）　　　　　　　図2　偶応力（単位面積当たりの偶力））

このマイクロポーラ材料の最適な構造をシミュレーションしています．

解析例

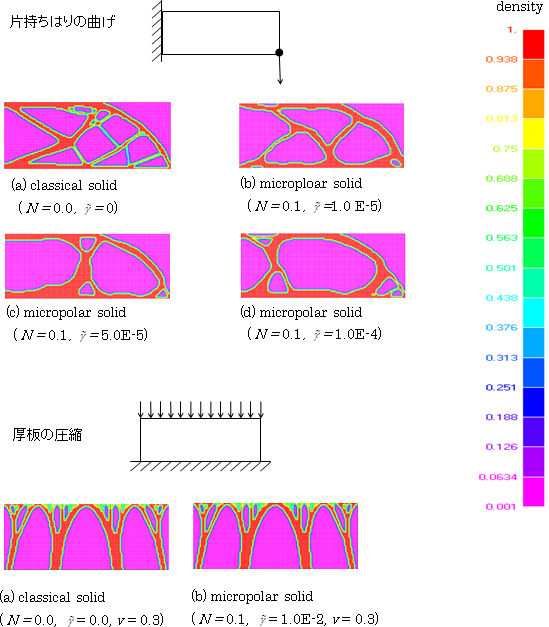
「片持ちはり」の問題では，古典弾性論における最適構造は「トラス構造」になり，より曲がり難い材料では「ラーメン構造」になります．「厚板の圧縮」の問題ではいずれの材料においても最適構造に差はなく，アーチ構造が現れます．